|
A continuación se presentan las habilidades específicas vinculadas con el problema desarrollado y la aproximación de áreas, así como otros elementos didácticos pertinentes. |
A continuación se presentan las habilidades específicas vinculadas con el problema desarrollado y la "Aproximación de áreas", así como otros elementos didácticos pertinentes.
Habilidades específicas que se trabajan con el problema
A través del problema Zacate para el jardín se trabajó un tema que pertenece a Polígonos, de décimo año, incluye el estudio perímetros y áreas de figuras planas no poligonales utilizando coordenadas rectangulares.
En general este tema incluye las siguientes habilidades específicas:
14. Calcular perímetro y áreas de polígonos no regulares utilizando un sistema de coordenadas rectangulares (MEP, 2012, p. 389).
26. Estimar perímetros y áreas de figuras planas no poligonales utilizando un sistema de coordenadas rectangulares (MEP, 2012, p. 391).
A través de la resolución del problema, el estudiante recurre a utilizar conocimientos previos como el área del rectángulo y trapecio.
El estudiante a través de la resolución emplea la segunda habilidad específica citada previamente, debido a que requiere transformar la imagen del jardín, la cual es irregular y amorfa, en figuras conocidas para poder aproximar el área.
Indicaciones metodológicas
Respecto a la organización de la lecciones, el MEP (2012, p. 41-44) establece dos etapas, el problema Zacate para el jardín puede ser empleado en la II Etapa: La movilización y aplicación de los conocimientos, debido a que los estudiantes están en la capacidad de usar la estrategia de aproximación mediante áreas de figuras planas conocidas desde la primaria, en 5º año se encuentra la habilidad específica:
4. Calcular perímetros y áreas de figuras planas compuestas por triángulos, cuadrados, rectángulos, paralelogramos y trapecios (MEP, 2012, p. 205).
Por tanto, este problema no debe representar una novedad. Sin embargo, queda a criterio del docente, de acuerdo con las características de sus estudiantes, valorar si es pertinente emplearlo para la I Etapa.
De acuerdo con la MEP (2012, p. 400) se deben tener los siguiente aspectos en consideración:
-
El estudio de las áreas puede ser abordado mediante la Historia. Por ejemplo, Arquímedes de Siracusa aproximó el valor del número π . Para ello dibujó un polígono regular inscrito y otro circunscrito a una misma circunferencia, de manera que la longitud de la circunferencia y el área del círculo quedan acotadas por esos mismos valores de las longitudes y las áreas de los dos polígonos. A medida que se incrementa el número de lados del polígono la diferencia se acorta y se obtiene una aproximación más exacta. Partiendo de polígonos de 96 lados cada uno, Arquímedes calculó que el valor de π debía encontrarse entre 3 y 10 ⁄ 71 (aproximadamente 3,1408) o 3 y 1/7 (aproximadamente 3,1429), lo cual es consistente con el valor real de π.
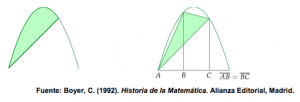
A esta técnica se le conoce con el nombre de método de exhaución. También, demostró que el área del segmento parabólico de la figura que aparece abajo a la izquierda es igual a 4/3 de la del triángulo inscrito de la figura de abajo a la derecha.
Nivel de complejidad y procesos matemáticos