Introducción a las funciones: Glosario

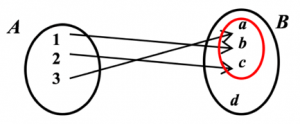
Dado una función $f$ entre dos conjuntos no vacíos $A$ y $B$, el conjunto de entradas $A$ se conoce como dominio mientras que el conjunto $B$ se denomina codominio o contradominio de la función.

Es usual dar únicamente la forma simbólica de la regla de correspondencia de una función, es decir, el criterio de la función: $y=f(x)$ sin especificar su dominio. En este caso se considera como dominio de la función el conjunto de todos los valores reales que pueden ser asignados a la variable independiente $x$ de tal forma que la variable dependiente $y$ resulte un número real único y se conoce como dominio máximo o dominio natural.

Dado una función $f$ con dominio $A$ y codominio $B$, si $y in B$ y si existe $x in A$ tal que $y=f(x)$ entonces el elemento y se denomina imagen de $x$. También se dice que $x$ es preimagen de $y$.

Dado una función $f$ con dominio $A$ y codominio $B$ el conjunto de las imágenes de los elementos del dominio se denomina rango, ámbito o recorrido de la función. El rango es un subconjunto del codominio de una función. Si representamos el rango de $f$ con el símbolo $R_{f}$ entonces podemos escribir:

$R_{f}={y/ y in B, textrm{tal que} y=f(x), textrm{para algún elemento} x in A }$. Por ejemplo, si $A={1,2,3}$ es el dominio de una función $f$ y $B={a,b,c,d}$ es su codominio y la regla de asociación entre los elementos de $A$ y de $B$ es representada por el diagrama de Venn que sigue:

entonces el rango de f es el conjunto $R_{f}={a,b,c}$ . En este caso $din B$ pero $d notin R_{f}$ pues no existe elemento de $A$ cuya imagen es el elemento $d$.

Si alguna recta vertical interseca la curva en más de un punto entonces la gráfica no corresponde a una función.

La gráfica de una función real de una variable real $f$ es el conjunto de los puntos $(x,y)$ del plano cartesiano donde la variable independiente $x$ pertenece al dominio de la función y la variable dependiente $y$ satisface $y=f(x)$, es decir, $y$ es la imagen de $x$ al aplicar la regla de correspondencia $f$.

Una función con representación simbólica $y=f(x)$ es creciente en un intervalo abierto A si para cualquier par de puntos $a$ y $b$ de $A$ tales que $a<b$ se cumple que $f(a)<f(b)$.

Esto significa que una función es creciente si al aumentar el valor de la variable independiente $x$, el valor de la variable dependiente $y$ también aumenta. En una representación gráfica esto puede verse cuando al avanzar de izquierda a derecha observamos que la gráfica va “subiendo”.

Una función con representación simbólica $y=f(x)$ es decreciente en un intervalo abierto $A$ si para cualquier par de puntos $a$ y $b$ de $A$ tales que $a<b$ se cumple que $f(a)>f(b)$.

En otras palabras, una función es decreciente si al aumentar el valor de la variable independiente $x$, el valor de la variable dependiente $y$ disminuye. En una representación gráfica esto puede verse cuando al avanzar de izquierda a derecha observamos que la gráfica va “bajando”.

Una función con representación simbólica $y=f(x)$ es constante en un intervalo abierto $A$ si existe una constante $c$ tal que $f(x)=c$ para todo valor de $x$ en $A$.

La función $f$ tiene un valor máximo relativo o local en el número $c$, si existe un intervalo abierto que contiene a $c$, en el que $f$ está definida, tal que $f(c) geq f(x)$ para toda $x$ en el intervalo.

La función $f$ tiene un valor mínimo relativo o local en el número $c$, si existe un intervalo abierto que contiene a $c$, en el que $f$ está definida, tal que $f(c) leq f(x)$ para toda $x$ en el intervalo.

En las definiciones anteriores tenemos que $f(c)$ es un valor máximo local si el punto $(c,f(c))$ es el punto más elevado en la representación gráfica de $f$, en algún intervalo abierto que contiene $c$. Igualmente, $f(c)$ es un valor mínimo local si el punto $(c,f(c))$ es el punto más bajo en la representación gráfica de $f$, en algún intervalo abierto que contiene $c$.

Una función con dominio $A$ es inyectiva (uno a uno) si no existen dos elementos distintos en $A$ que tengan la misma imagen, es decir, $f(a)neq f(b)$ siempre que $a neq b, ,, a, bin A$.

Una forma equivalente de escribir la condición de una función inyectiva es: Si $f(a)=f(b)$ con $a,b in A$ entonces $a=b$

Una función es inyectiva (uno a uno) si y sólo si ninguna recta horizontal interseca su gráfica más de una vez.