 |
A continuación se presentan las habilidades específicas vinculadas con la parte del tema de Diagrama de cajas relacionado con el problema desarrollado y otros elementos didácticos pertinentes. |
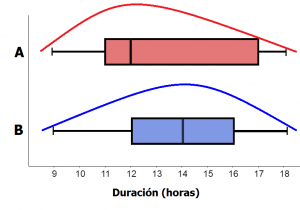
El problema “Duración de carga de celulares” puede ser útil para introducir la representación diagrama de cajas y a la vez propiciar la habilidad específica:
Utilizar diagramas de cajas para comparar la posición y la variabilidad de dos grupos de datos. (MEP, 2012, p. 438)
Se debe tomar en cuenta que en décimo año se desarrollan las siguientes habilidades que son la base para la introducción de los diagramas de cajas:
Resumir un grupo de datos mediante el uso de la moda, la media aritmética, la mediana, los cuartiles, el máximo y el mínimo, e interpretar la información que proporcionan dichas medidas. (MEP, 2012, p. 432)
Identificar la ubicación aproximada de las medidas de posición de acuerdo con el tipo de asimetría de la distribución de los datos. (MEP, 2012, p. 432)
Indicaciones metodológicas
El problema "Duración de carga de celulares" está planteado para la movilización y aplicación de los conocimientos, debido a que se debe conocer la representación gráfica dada en el contexto. Sin embargo, se puede cambiar esta representación por un cuadro con las principales medidas de orden que ya han sido estudiadas en décimo año y solicitar al estudiante que a partir de estas construyan una representación que involucrara estas medidas.
Ver ejemplo
Duración (en horas) de una muestra aleatoria
de 100 celulares de las marcas A y B
| Marca A | Marca B | |
| Mínimo | 9 | 9 |
| Primer cuartil | 11 | 12 |
| Mediana | 12 | 14 |
| Tercer cuartil | 17 | 16 |
| Máximo | 18 | 18 |
Haciendo esta modificación al problema, se podría introducir el diagrama de cajas a partir de los conocimientos previos. Asimismo, MEP (2012, p. 439) se debe considerar lo siguiente:
Se debe evidenciar la importancia de las medidas estadísticas tanto de posición como de variabilidad para representar características propias de los datos. Éstas se complementan con las representaciones tabulares y gráficas como estrategias para resumir la información que comunican los datos, para tener elementos suficientes que permitan argumentar sobre un problema particular.
Para la acción de aula, es importante tener presente el potencial que tienen los diagramas de cajas conectan las medidas de posición con las de variabilidad, por lo que se recomienda no solo enfatizar en la construcción del gráfico y el análisis de la variabilidad, sino que dentro de los análisis pueda complementar con estos otros elementos que caracterizan la posición y la forma de la distribución de los datos. Como por ejemplo describir una distribución de datos de acuerdo con el tipo de asimetría:
Nivel de complejidad y procesos matemáticos El nivel de complejidad del problema debe catalogarse como de conexión, debido a que con excepción del proceso de Plantear y resolver problemas, todos los otros procesos matemáticos intervinieron a un grado de complejidad intermedio. Este problema se puede emplear para la movilización y aplicación de los conocimientos (reforzar aprendizajes), por lo que bajo esta premisa los siguientes procesos matemáticos: Razonar y argumentar Se activa a un grado de complejidad intermedio, aunque la información se puede leer de forma directa del diagrama de cajas, se debe razonar y argumentar diferentes elementos a partir de este para la toma de decisiones. Plantear y resolver problemas Se activa a un grado de complejidad bajo al tener que resolver el problema mediante la interpretación de una representación que ya ha sido estudiada. Conectar Se activa a un grado complejidad intermedio ya que se crea una conexión entre una representación estadística que se presenta en una situación de contexto real. Comunicar Se activa a un grado complejidad intermedio al tener que vincular la duración de la carga de la batería y un diagrama de cajas, para luego a partir del análisis de las medidas de posición que se presentan en al representación gráfica brindar la respuesta al problema mediante lenguaje natural. Representar Se activa a un grado de complejidad intermedio al tener que leer y razonar a partir de las medidas de posición que se presenta en los diagramas de cajas.
Los contextos en Estadística y Probabilidad
Los fundamentos plasmados en los programas de estudio de Matemáticas promueven que la enseñanza de la Estadística se realice desde una perspectiva eminentemente práctica, que responde propiamente a la naturaleza de la disciplina. Por esta razón, la contextualización activa debe estar presente en la gran mayoría de los problemas que se planteen tanto para la acción de aula como para la evaluación. No obstante, en el componente de Probabilidad, al tener mayor cercanía con las otras áreas matemáticas, algunos de los problemas que se utilicen pueden responder a contextos matemáticos o lúdicos.
Una acotación adicional relacionada con la Estadística consiste en definirla como una disciplina constituida por diferentes métodos y técnicas que se relacionan con la recolección, organización, representación y resumen de datos, con el propósito de extraer conclusiones o inferencias sobre el contexto que da origen a estos datos. En este sentido, los programas de estudio profundizan en la parte de la estadística descriptiva que se relaciona con estrategias para la organización, representación y resumen de datos; pero no enfatiza en la recolección mediante muestreo estadístico y no incluye la inferencia estadística que permite realizar conclusiones y generalizaciones para la población total de los datos. Por esta razón, los diferentes problemas que se utilicen enfatizan en la descripción y análisis de datos en diferentes contextos; pero no así en la generalización de la información que describen esos datos. Esto quiere decir, que el énfasis de los análisis se centra en realizar una adecuada lectura de la información que comunican o describen los datos sobre el contexto.